Analysis of duality-based interconnected kinematics of planar serial and parallel manipulators using screw theory

Abstract

In this paper, a method has been proposed to analyze the planar architectures of serial and parallel manipulators, based on the duality associated with their interconnected kinematics. The interconnected kinematics states that model of one architecture can be derived from the kinematic model of the other, using screw theory approach. The performance of the initial and the derived manipulators was evaluated with three criteria: isotropy, maximum force transmission ratio and local transmission index. Without loss of generality, the serial manipulator derived from parallel has better isotropy, while the parallel manipulator derived from serial can be designed to have better force and power transmission.

Appendix

1.1 Inverse of matrix having axis coordinates

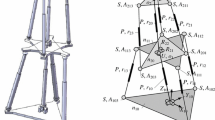
Consider three lines $\hat{S}_{1} ,\,\,\hat{S}_{2} ,$ and $\hat{S}_{3}$ having coordinates ($x_{1}$, $y_{1}$), ($x_{2}$, $y_{2}$) and ($x_{3}$, $y_{3}$) as shown in Fig. 23. The matrix Q can be written as

Fig. 23

Three lines in XY plane

$$ Q = \left[ {\begin{array}{*{20}c} {\hat{S}_{1} } & {\hat{S}_{2} } & {\hat{S}_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {y_{1} } & {y_{2} } & {y_{3} } \\ { - x_{1} } & { - x_{2} } & { - x_{3} } \\ 1 & 1 & 1 \\ \end{array} } \right]. $$

(64)

The inverse of $Q$ can be expressed as

$$ Q^{ - 1} = Q^{{{\prime }T}} /\det Q. $$

(65)

Adjoint matrix can be constructed as follows

$$ Q^{{\prime }} = \left[ {\begin{array}{*{20}c} {x_{3} - x_{2} } & {x_{1} - x_{3} } & {x_{2} - x_{1} } \\ {y_{3} - y_{2} } & {y_{1} - y_{3} } & {y_{2} - y_{1} } \\ {x_{2} y_{3} - x_{3} y_{2} } & {x_{3} y_{1} - x_{1} y_{3} } & {x_{1} y_{2} - x_{2} y_{1} } \\ \end{array} } \right]. $$

(66)

Substituting (66) into (65), we get

$$ Q^{ - 1} = \left[ {\begin{array}{*{20}c} {x_{3} - x_{2} } & {x_{1} - x_{3} } & {x_{2} - x_{1} } \\ {y_{3} - y_{2} } & {y_{1} - y_{3} } & {y_{2} - y_{1} } \\ {x_{2} y_{3} - x_{3} y_{2} } & {x_{3} y_{1} - x_{1} y_{3} } & {x_{1} y_{2} - x_{2} y_{1} } \\ \end{array} } \right]^{T} /\det Q. $$

(67)

Let $\hat{s}_{2} ,$$\hat{s}_{3}$ and $\hat{s}_{1}$ are the column vectors formed by the unitized coordinates of the lines joining the points 2-3, 3-1 and 1-2, respectively, where $u_{23}$ given by

$$ u_{23} = \sqrt {(x_{3} - x_{2} )^{2} + (y_{3} - y_{2} )^{2} } $$

(68)

is denoted as the distance between two points. Then,

$$ \left[ {\left( {x_{3} - x_{2} } \right),\left( {y_{3} - y_{2} } \right);\left( {x_{2} y_{3} - x_{3} y_{2} } \right)\,} \right]\, = u_{23} \hat{s}_{2} , $$

(69)

where $\hat{s}_{2}^{T} = \left[ {c_{2} ,s_{2} ;\,p_{2} } \right].$

Now, (65) can be expressed as

$$ Q^{ - 1} = \left[ \begin{aligned} u_{23} \hat{s}_{2}^{T} \hfill \\ u_{31} \hat{s}_{3}^{T} \, \hfill \\ u_{12} \hat{s}_{1}^{T} \hfill \\ \end{aligned} \right]/\det Q, $$

(70)

where

$$ \begin{aligned} \det Q &= y_{1} (x_{3} - x_{2} ) - x_{1} (y_{3} - y_{2} ) + 1(x_{2} y_{3} - x_{3} y_{2} )\\ &= \hat{S}_{1}^{T} u_{23} \hat{s}_{2} = u_{23} \hat{s}_{2}^{T} \hat{S}_{1} . \hfill \\ \end{aligned} $$

(71)

Similarly,

$$ \det Q = \hat{S}_{2}^{T} u_{31} \hat{s}_{3} = u_{31} \hat{s}_{3}^{T} \hat{S}_{2} $$

(72)

$$ \det Q = \hat{S}_{3}^{T} u_{12} \hat{s}_{1} = u_{12} \hat{s}_{1}^{T} \hat{S}_{3} . $$

(73)

Finally, substituting (71) through (73) into (70), we have

$$ Q^{ - 1} = \left[ \begin{aligned} \frac{{\hat{s}_{2}^{T} }}{{\hat{s}_{2}^{T} \hat{S}_{1} }} \hfill \\ \frac{{\hat{s}_{3}^{T} }}{{\hat{s}_{3}^{T} \hat{S}_{2} }}\, \hfill \\ \frac{{\hat{s}_{1}^{T} }}{{\hat{s}_{1}^{T} \hat{S}_{3} }} \hfill \\ \end{aligned} \right], $$

(74)

where $\hat{s}_{1}^{T} = \left[ {c_{1} ,s_{1} ;p_{1} } \right]$, $\hat{s}_{2}^{T} = \left[ {c_{2} ,s_{2} ;p_{2} } \right]$ and $\hat{s}_{3}^{T} = \left[ {c_{3} ,s_{3} ;p_{3} } \right].$

It is noted that the three rows of (74) are lines expressed in ray coordinates. Therefore, it is remarked that the initial matrix $Q$ composed of three lines expressed by axis coordinate is converted into ray coordinate as a result of matrix inversion.

1.2 Inverse of matrix having ray coordinates

Assume that we have three lines $\hat{s}_{1} ,\,\,\hat{s}_{2}$ and $\hat{s}_{3}$ in plane as shown in Fig. 23. They can be expressed in ray coordinate. The matrix E having ray coordinates can be written as follows

$$ E = \left[ {\begin{array}{*{20}c} {c_{1} } &\quad {c_{2} } &\quad {c_{3} } \\ {s_{1} } &\quad {s_{2} } &\quad {s_{3} } \\ {p_{1} } &\quad {p_{2} } &\quad {p_{3} } \\ \end{array} } \right]. $$

(75)

Then, the inverse of $E$ can be expressed in the following way

$$ E^{ - 1} = E^{{{\prime }T}} /\det E $$

(76)

and it adjoint matrix can be constructed as follows

$$ E^{{\prime }} = \left[ {\begin{array}{*{20}c} {(s_{2} p_{3} - s_{3} p_{2} )} & {(s_{3} p_{1} - s_{1} p_{3} )} & {(s_{1} p_{2} - s_{2} p_{1} )} \\ { - (c_{2} p_{3} - c_{3} p_{2} )} & { - (c_{3} p_{1} - c_{1} p_{3} )} & { - (c_{1} p_{2} - c_{2} p_{1} )} \\ {(c_{2} s_{3} - c_{3} s_{2} )} & {(c_{3} s_{1} - c_{1} s_{3} )} & {(c_{1} s_{2} - c_{2} s_{1} )} \\ \end{array} } \right]. $$

(77)

Using Grassmann’s expansion given in (12) through (14), the point of intersection $(x_{1} ,y_{1} )\,$ of lines $\hat{s}_{1} ,\,\,\hat{s}_{2}$ can be solved by

$$ y_{1} : - x_{1} :1 = (s_{1} p_{2} - s_{2} p_{1} ): - (c_{1} p_{2} - c_{2} p_{1} ):(c_{1} s_{2} - c_{2} s_{1} ). $$

(78)

Rearranging (78) would result in

$$ \left[ \begin{aligned} (s_{1} p_{2} - s_{2} p_{1} ) \hfill \\ - (c_{1} p_{2} - c_{2} p_{1} ) \hfill \\ (c_{1} s_{2} - c_{2} s_{1} ) \hfill \\ \end{aligned} \right] = s_{2 - 1} \left[ \begin{aligned} y_{1} \hfill \\ - x_{1} \hfill \\ 1 \hfill \\ \end{aligned} \right] = s_{2 - 1} \hat{S}_{1} . $$

(79)

Similarly, the first and the second columns of (77) can be expressed, respectively, as

$$ \left[ \begin{aligned} (s_{2} p_{3} - s_{3} p_{2} ) \hfill \\ - (c_{2} p_{3} - c_{3} p_{2} ) \hfill \\ (c_{2} s_{3} - c_{3} s_{2} ) \hfill \\ \end{aligned} \right] = s_{3 - 2} \left[ \begin{aligned} y_{2} \hfill \\ - x_{2} \hfill \\ 1 \hfill \\ \end{aligned} \right] = s_{3 - 2} \hat{S}_{2} $$

(80)

and

$$ \left[ \begin{aligned} (s_{3} p_{1} - s_{1} p_{3} ) \hfill \\ - (c_{3} p_{1} - c_{1} p_{3} ) \hfill \\ (c_{3} s_{1} - c_{1} s_{3} ) \hfill \\ \end{aligned} \right] = s_{3 - 1} \left[ \begin{aligned} y_{3} \hfill \\ - x_{3} \hfill \\ 1 \hfill \\ \end{aligned} \right] = s_{3 - 1} \hat{S}_{3} . $$

(81)

Putting (79) through (81) into (76), we can get

$$ E^{ - 1} = \left[ \begin{aligned} s_{3 - 2} \hat{S}_{2}^{T} \hfill \\ s_{1 - 3} \hat{S}_{3}^{T} \, \hfill \\ s_{2 - 1} \hat{S}_{1}^{T} \hfill \\ \end{aligned} \right]/\det E. $$

(82)

Expanding determinant with respect to the first column of (77), we have

$$ \begin{aligned} \det E & = c_{1} (s_{2} p_{3} - s_{3} p_{2} ) - s_{1} (c_{2} p_{3} - c_{3} p_{2} ) + p_{1} (c_{2} s_{3} - c_{3} s_{2} ) \\ & = s_{3 - 2} \hat{S}^{T}_{2} \hat{s}^{{}}_{1} . \\ \end{aligned} $$

(83)

Similarly, for the second and third columns, we have

$$ \det E = s_{1 - 3} \hat{S}^{T}_{3} \hat{s}_{2} $$

(84)

$$ \det E = s_{2 - 1} \hat{S}^{T}_{1} \hat{s}_{3} . $$

(85)

Finally, inserting (83) through (85) into (82), we have

$$ E^{ - 1} = \left[ \begin{aligned} \frac{{\hat{S}_{2}^{T} }}{{\hat{S}^{T}_{2} \hat{s}_{1} }} \hfill \\ \frac{{\hat{S}_{3}^{T} }}{{\hat{S}^{T}_{3} \hat{s}_{2} }}\, \hfill \\ \frac{{\hat{S}_{1}^{T} }}{{\hat{S}^{T}_{1} \hat{s}_{3} }} \hfill \\ \end{aligned} \right]. $$

(86)

It is noted that the three rows of (86) are lines expressed in axis coordinates. Therefore, it is remarked that the initial matrix $E$ composed of three lines expressed by ray coordinate is converted into lines in axis coordinate as a result of matrix inversion.